零零碎碎的算法题

内存序	描述	典型场景
`relaxed`	只保证原子性，无顺序约束	计数器累加
`consume`	依赖该原子变量的后续操作必须在其后执行（已弃用）	很少使用
`acquire`	当前线程中后续读写操作必须在其之后执行	锁获取
`release`	当前线程中先前读写操作必须在其之前执行	锁释放
`acq_rel`	`acquire` + `release` 的结合	读-改-写操作
`seq_cst`	全局顺序一致性（性能最低但最安全）	需要严格顺序的场景

特性	赋值拷贝	移动拷贝
资源处理	深拷贝	资源所有权转移
原对象状态	保持不变	有效但未定义状态
性能	较高开销	低开销
使用场景	需要独立副本时	临时对象或明确不需要原对象时
触发方式	`=` 或显式拷贝	`std::move()` 或临时对象

LRU

题目来源： 146. LRU 缓存

请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。

实现 LRUCache 类：

LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

我们使用双向链表+哈希表的方式进行实现

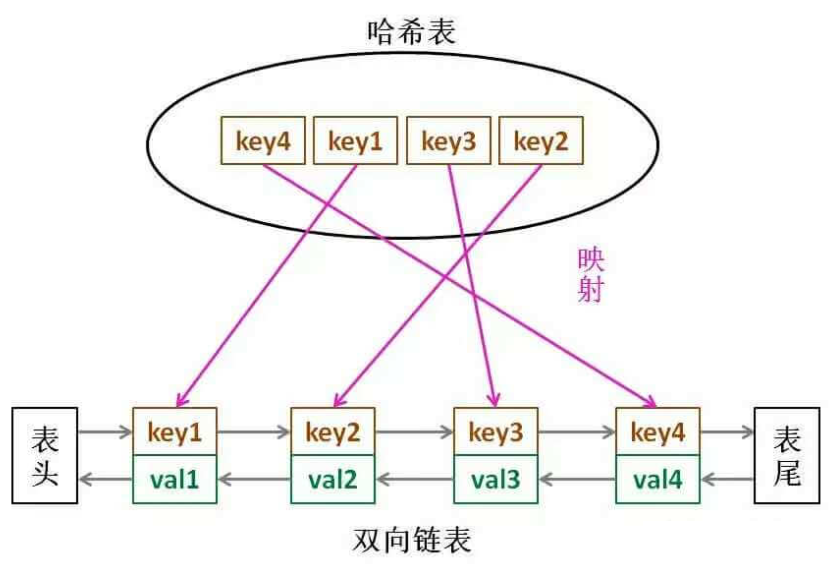
get : 若存在节点就将其删除后放到表头即可
put : 先判断是否存在，存在的话将其值更新一下放到表头即可；不存在的话需要创建一个节点放到表头，之后还需要判断数量是否超出，超出则从表尾删除即可

综上，我们可以提取以下几个函数：

删除一个节点
在表头新增一个节点
寻找指定的节点

自实现双链表

#include <bits/stdc++.h>

// 双链表节点结构
struct Node {
    int key;
    int value;
    Node *prev;
    Node *next;

    Node(int k = 0, int v = 0) : key(k), value(v), prev(nullptr), next(nullptr) {
    }
};

class LRUCache {
private:
    Node *dummy;
    int capacity;
    std::unordered_map<int, Node *> map; // 哈希表存储key到节点的映射

    // 在双链表中删除当前节点（不释放内存）
    void removeNode(Node *node) {
        node->prev->next = node->next;
        node->next->prev = node->prev;
    }

    // 将节点插入到链表头部（dummy节点之后）
    void pushFront(Node *node) {
        node->prev = dummy;
        node->next = dummy->next;
        node->next->prev = node;
        dummy->next = node;
    }

    // 根据key查找节点，找到则移动到表头
    Node *getNode(int key) {
        auto it = map.find(key);
        if (it == map.end()) {
            return nullptr; // key不存在
        }
        // 将访问的节点移到链表头部
        removeNode(it->second);
        pushFront(it->second);
        return it->second;
    }

public:
    LRUCache(int capacity) : capacity(capacity) {
        dummy = new Node();
        dummy->prev = dummy; // 初始时自循环
        dummy->next = dummy;
    }

    // 析构函数释放所有节点内存
    ~LRUCache() {
        Node *curr = dummy->next;
        while (curr != dummy) {
            Node *temp = curr;
            curr = curr->next;
            delete temp;
        }
        delete dummy;
    }

    // 获取key对应的value（不存在返回-1）
    int get(int key) {
        auto node = getNode(key);
        return node ? node->value : -1;
    }

    void put(int key, int value) {
        auto node = getNode(key); // 自动移到表头
        if (node) {
            node->value = value; // 存在则更新值
            return;
        }

        // 创建新节点（注意参数顺序：key, value）
        auto newNode = new Node(key, value);
        pushFront(newNode); // 插入链表头部
        map[key] = newNode; // 加入哈希表

        // 超过容量时淘汰最久未使用的节点
        if (map.size() > capacity) {
            auto backNode = dummy->prev; // 链表尾部是最久未使用的
            removeNode(backNode);
            map.erase(backNode->key);
            delete backNode;
        }
    }
};

stl::list实现

我们可以使用自带的stl容器，其中哈希表保存相应节点的迭代器，就可以直接操作啦，在这之前复习一下之前的函数 splice

void splice(const_iterator pos, list& other, const_iterator it);

作用：将 other 链表中 it 指向的节点移动到 *this 链表的 pos 位置之前。
关键特性：
- 仅修改节点间的指针链接，不涉及数据的拷贝或移动。
- 时间复杂度 O(1)。
参数说明：

参数	含义
`pos`	目标位置（新链表中的插入位置，插入到 `pos` 之前）
`other`	源链表（可以是另一个链表，也可以是当前链表自身）
`it`	源链表中待移动的节点迭代器（必须指向 `other` 中的有效节点）

代码实现：

class LRUCache {
public:
    LRUCache(int capacity) : cap(capacity) {}

    int get(int key) {
        auto it = map.find(key);
        if (it == map.end()) return -1;

        // 将节点移到链表头部
        cache.splice(cache.begin(), cache, it->second);
        return it->second->second;
    }

    void put(int key, int value) {
        auto it = map.find(key);
        if (it != map.end()) {
            // 更新值并移到头部
            it->second->second = value;
            //将cache链表中的迭代器it->second移动到cache的表头
            cache.splice(cache.begin(), cache, it->second);
            return;
        }

        //如果容量已满，先删除尾部节点
        if (cache.size() == cap) {
            map.erase(cache.back().first);
            cache.pop_back();
        }
        //插入新节点
        cache.emplace_front(key, value);
        map[key] = cache.begin();
    }

private:
    int cap;
    std::list<std::pair<int, int>> cache;
    std::unordered_map<int, std::list<std::pair<int, int>>::iterator> map;
};

LFU

题目来源：460. LFU 缓存

请你为最不经常使用（LFU）缓存算法设计并实现数据结构。

实现 LFUCache 类：

LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
int get(int key) - 如果键 key 存在于缓存中，则获取键的值，否则返回 -1 。
void put(int key, int value) - 如果键 key 已存在，则变更其值；如果键不存在，请插入键值对。当缓存达到其容量 capacity 时，则应该在插入新项之前，移除最不经常使用的项。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除 最久未使用 的键。

为了确定最不常使用的键，可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。

当一个键首次插入到缓存中时，它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作，使用计数器的值将会递增。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

LRU的实现是一个哈希表加上一个双链表
而LFU则要复杂多了，需要用两个哈希表再加上N个双链表才能实现

第一个哈希表用来存储key和node节点的映射：

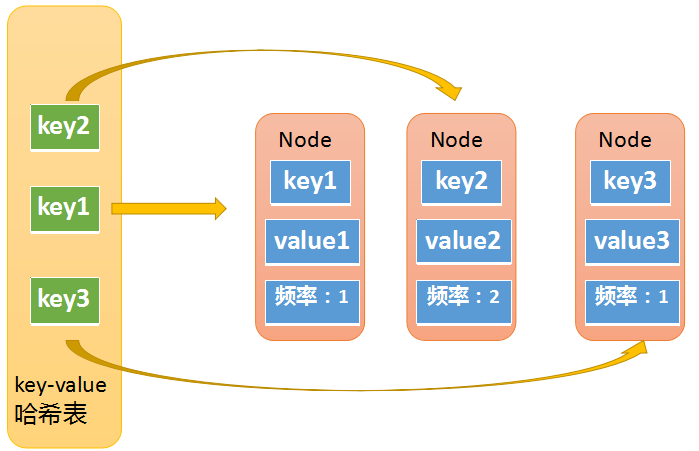
第二个哈希表存储了访问频率和节点的映射，保存的是一个双链表

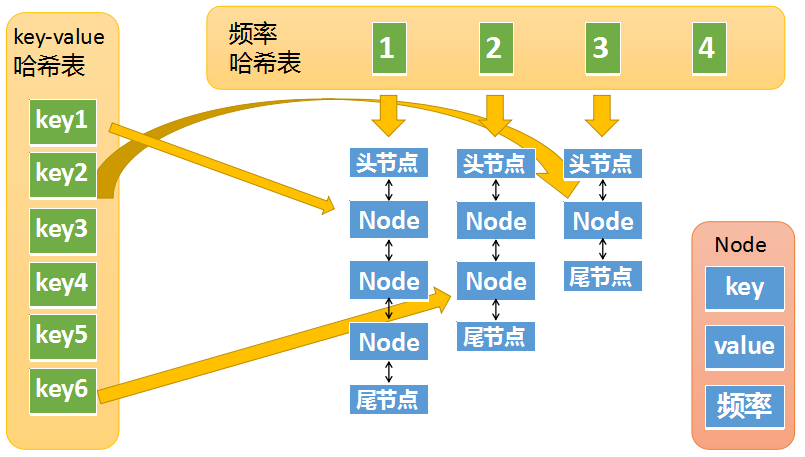
get操作的具体逻辑大致是这样：
- 如果key不存在则返回-1
- 如果key存在，则返回对应的value，同时:
  - 将元素的访问频率+1
    - 将元素从访问频率 i 的链表中移除，放到频率 i+1 的链表中
    - 如果频率i的链表为空，则从频率哈希表中移除这个链表
put 操作就要复杂多了，大致包括下面几种情况
- 如果key已经存在，修改对应的value，并将访问频率+1
  - 将元素从访问频率i的链表中移除，放到频率i+1的链表中
  - 如果频率i的链表为空，则从频率哈希表中移除这个链表
- 如果key不存在
  - 缓存超过最大容量，则先删除访问频率最低的元素，再插入新元素
    新元素的访问频率为1，如果频率哈希表中不存在对应的链表需要创建
  - 缓存没有超过最大容量，则插入新元素
    新元素的访问频率为1，如果频率哈希表中不存在对应的链表需要创建
我们在代码实现中还需要维护一个minFreq 的变量，用来记录LFU缓存中频率最小的元素，在缓存满的时候，可以快速定位到最小频繁的链表，以达到 O(1) 时间复杂度删除一个元素。
具体做法是:
- 更新/查找的时候，将元素频率+1，之后如果min_freq不在频率哈希表中了，说明频率哈希表中已经没有元素了，那么min_freq需要+1，否则min_freq不变。
- 插入的时候，这个简单，因为新元素的频率都是1，所以只需要将min_freq改为1即可。

#include <bits/stdc++.h>

struct Node {
    int key;
    int value;
    int freq = 1;
    Node *prev;
    Node *next;

    Node(int key = 0, int value = 0)
        : key(key), value(value) {
    }
};

class LFUCache {
private:
    int min_freq;
    int capacity;
    std::unordered_map<int, Node *> key_to_node;
    std::unordered_map<int, Node *> freq_to_list;

    void removeNode(Node *node) {
        node->prev->next = node->next;
        node->next->prev = node->prev;
    }

    Node *newListDummy() {
        auto dummy = new Node();
        dummy->next = dummy;
        dummy->prev = dummy;
        return dummy;
    }

    /**
     * 将节点node添加到freq对应的双向链表表头，
     * 我们可确认的是node在对应的哈希标中，该函数仅作填充到表头操作（若不存在则创建一个）
     * @param freq 频率
     * @param node 待添加节点
     */
    void pushFront(int freq, Node *node) {
        // 查找频率对应的双向链表，不存在则创建并添加到哈希表中
        auto dummy=freq_to_list[freq];
        if (dummy==nullptr) {
            dummy = newListDummy();
            freq_to_list[freq] = dummy;
        }

        // 建立链接
        node->prev = dummy;
        node->next = dummy->next;
        node->prev->next = node;
        node->next->prev = node;
    }

    Node *getNode(int key) {
        auto it = key_to_node.find(key);
        if (it == key_to_node.end()) {
            return nullptr;
        }
        Node* node = it->second;
        removeNode(node);
        // 检查该节点的链表是否为空，为空这删除整个链表
        auto dummy = freq_to_list[node->freq];
        if (dummy == dummy->prev) {
            // 空的，删除链表
            freq_to_list.erase(node->freq);
            delete dummy;
            // 更新一下最小频率
            // 该条件语句也满足的话，说明node频率为最小且仅有这一个
            // node删除后，最小频率也该更新一下了
            if (min_freq == node->freq) {
                min_freq++;
            }
        }
        // 将node放到指定的node->freq的链表上
        pushFront(++node->freq, node);
        return node;
    }

public:
    LFUCache(int capacity) : capacity(capacity) {
    }

    int get(int key) {
        auto node = getNode(key);
        return node ? node->value : -1;
    }

    void put(int key, int value) {
        // 直接查询是否存在
        auto node = getNode(key);
        // 存在的话，更新值就行了
        if (node) {
            node->value = value;
            return;
        }
        // 不存在的话，判断是不是满了
        if (key_to_node.size() == capacity) {
            // 先删除频率 最低 的 最后 一个节点
            auto dummy = freq_to_list[min_freq];
            auto backNode = dummy->prev;
            key_to_node.erase(backNode->key);
            removeNode(backNode);
            delete backNode;
            // 到这算是删除了最后一个节点，不过删除后链表是否为空呢？
            // 进一步判断
            if (dummy == dummy->prev) {
                freq_to_list.erase(min_freq);
                delete dummy;
                // 这里就不用像getNode一样判断了，频率肯定是最小的
            }
        }
        // 有空间了，创建一个新节点放到频率为1的双链表上就行
        key_to_node[key] = node = new Node(key, value);
        pushFront(1, node);
        min_freq = 1;
    }
};

环形缓冲区

线程池

shared_ptr

在实现代码之前，了解两个小知识点：内存序和移动语义。

内存序是多线程编程中控制原子操作执行顺序的关键机制，用于解决可见性和顺序性问题。
1. 为什么需要内存序？
硬件优化：CPU 会乱序执行指令（如写缓冲、指令重排）
编译器优化：编译器可能调整代码顺序
多核一致性：不同核心的缓存可能不一致
2. 六种内存序及其用途
内存序描述典型场景
relaxed 只保证原子性，无顺序约束计数器累加
consume 依赖该原子变量的后续操作必须在其后执行（已弃用）很少使用
acquire 当前线程中后续读写操作必须在其之后执行锁获取
release 当前线程中先前读写操作必须在其之前执行锁释放
acq_rel acquire + release 的结合读-改-写操作
seq_cst 全局顺序一致性（性能最低但最安全）需要严格顺序的场景

内存序	描述	典型场景
`relaxed`	只保证原子性，无顺序约束	计数器累加
`consume`	依赖该原子变量的后续操作必须在其后执行（已弃用）	很少使用
`acquire`	当前线程中后续读写操作必须在其之后执行	锁获取
`release`	当前线程中先前读写操作必须在其之前执行	锁释放
`acq_rel`	`acquire` + `release` 的结合	读-改-写操作
`seq_cst`	全局顺序一致性（性能最低但最安全）	需要严格顺序的场景

赋值拷贝
创建一个对象的完整副本，原对象和新对象独立存在
调用拷贝构造函数或拷贝赋值运算符
对资源(如动态内存)进行深拷贝
原对象保持不变
移动拷贝
将资源从一个对象"转移"到另一个对象，原对象进入有效但未定义状态
调用移动构造函数或移动赋值运算符
对资源进行浅拷贝，然后使原对象放弃资源所有权
原对象通常会被置空或处于可析构状态
特性赋值拷贝移动拷贝
资源处理深拷贝资源所有权转移
原对象状态保持不变有效但未定义状态
性能较高开销低开销
使用场景需要独立副本时临时对象或明确不需要原对象时
触发方式 = 或显式拷贝 std::move() 或临时对象
对于shared_ptr来说，拷贝增加计数，移动不改变计数。

特性	赋值拷贝	移动拷贝
资源处理	深拷贝	资源所有权转移
原对象状态	保持不变	有效但未定义状态
性能	较高开销	低开销
使用场景	需要独立副本时	临时对象或明确不需要原对象时
触发方式	`=` 或显式拷贝	`std::move()` 或临时对象

代码实现：

#include <atomic>

template<typename T>
class shared_ptr {
private:
    T *ptr; // 原始指针，指向管理的对象
    std::atomic<int> *ref_count; // 原子引用计数器
    // 释放资源：减少引用计数，若计数归零则销毁对象和计数器
    void release() const {
        if (ref_count && ref_count->fetch_sub(1, std::memory_order_acq_rel) == 1) {
            delete ptr;
            delete ref_count;
        }
    }

public:
    shared_ptr(): ptr(nullptr), ref_count(nullptr) {
    }

    //防止隐式类型转换
    explicit shared_ptr(T *ptr) : ptr(ptr), ref_count(new std::atomic<int>(1)) {
    }

    ~shared_ptr() {
        release();
    }

    // 拷贝构造函数：共享所有权（增加引用计数）
    shared_ptr(const shared_ptr<T> &other): ptr(other.ptr), ref_count(other.ref_count) {
        if (ref_count) {
            ref_count->fetch_add(1, std::memory_order_relaxed);
        }
    }

    // 拷贝赋值运算符：先释放旧资源，再共享新资源
    shared_ptr &operator=(const shared_ptr<T> &other) {
        if (this != &other) {
            release();
            ptr = other.ptr;
            ref_count = other.ref_count;
            if (ref_count) {
                ref_count->fetch_add(1, std::memory_order_relaxed);
            }
        }
    }

    // 移动构造函数：接管资源所有权（不修改引用计数）
    shared_ptr(shared_ptr<T> &&other) noexcept: ptr(other.ptr), ref_count(other.ref_count) {
        other.ptr = nullptr;
        other.ref_count = nullptr;
    }

    // 移动赋值运算符：先释放旧资源，再接管新资源
    shared_ptr &operator=(shared_ptr<T> &&other) noexcept {
        if (this != &other) {
            release();
            ptr = other.ptr;
            ref_count = other.ref_count;
            other.ptr = nullptr;
            other.ref_count = nullptr;
        }
        return *this;
    }

    //解引用运算符
    T &operator*() const {
        return *ptr;
    }

    T *operator->() const {
        return ptr;
    }

    T *get() const {
        return ptr;
    }

    int get_ref_count() const {
        return *ref_count ? ref_count->load(std::memory_order_acquire) : 0;
    }

    // 重置指针：释放旧资源，可选绑定新资源
    void reset(T *p = nullptr) {
        release();
        ptr = p;
        ref_count = p ? new std::atomic<int>(1) : nullptr;
    }
};

测试代码：

#include <vector>
#include <thread>
#include <iostream>
int main() {
    shared_ptr<int> ptr(new int(42));
    const int num_threads = 10;
    std::vector<std::thread> threads;
    for (int i = 0; i < num_threads; i++) {
        threads.emplace_back([&ptr]()-> void {
            for (int j = 0; j < 10000; j++) {
                shared_ptr<int> local_ptr(ptr);
                std::this_thread::sleep_for(std::chrono::milliseconds(3));
                std::cout << ptr.get_ref_count() << std::endl;
            }
        });
    }
    for (auto &t: threads) {
        t.join();
    }
    std::cout << "use_count:" << ptr.get_ref_count() << std::endl;
    if (ptr.get_ref_count() == 1) {
        std::cout << "Test OK" << std::endl;
    } else {
        std::cout << "Test Fail" << std::endl;
    }
}

零零碎碎的算法题

阅读选项

LRU

自实现双链表

stl::list实现

LFU

环形缓冲区

线程池

shared_ptr

1. 为什么需要内存序？

2. 六种内存序及其用途

赋值拷贝

移动拷贝

单例模式

定时器

LRU

自实现双链表

stl::list实现

LFU

环形缓冲区

线程池

shared_ptr

1. 为什么需要内存序？

2. 六种内存序及其用途

赋值拷贝

移动拷贝

单例模式

定时器

微信分享二维码

猜您想看

二分查找

十大排序算法

二叉树的遍历

评论区(暂无评论)

我要评论

这里空空如也，快来评论吧~

支持作者